
Predictions
We constantly make predictions about the future—ranging from everyday events to global trends—based on past information, knowing some outcomes are more predictable than others and all are inherently uncertain.
the formula
\(P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)}\)
\(P(A \mid B)\) is probability A given some additional information.
Medical Testing terminology
A test is 99% sensitive and 99% accurate.
i.e. false +ve rate of 99% and false negative rate of 99%
beliefs, rationality and bayesian brains
Our brains are perhaps bayesian. it is why two people can look at the same evidence and come to the same conclusion. Our existing beliefs mean our rational decision making comes to different conclusion to someone else.
Medical Testing Example
Mammogram 80% sensitive, 90% specific. a positive test result, what are the chances got it ? we have absolutely no idea unless we have some belief about the population.
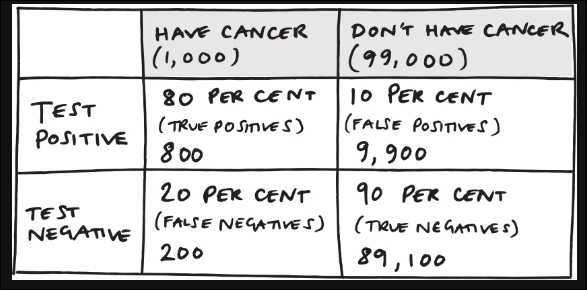
the chances are about \(\frac{800}{9900 + 800} \approx 0.07\)
changing the situation to a more illness prone population the percentages change drastically
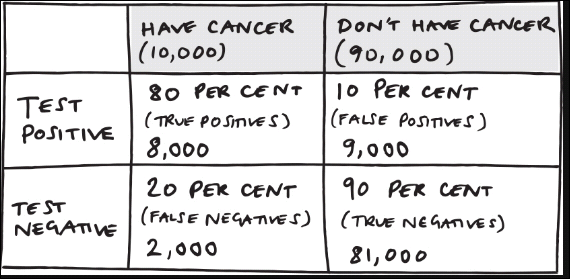
we easily confuse \(P(A \mid B)\) and \(P(B \mid A)\)
we want probability of cancer given positive test result \(P(A \mid B)\)
but instead we have got \(P(B \mid A)\)
the probability of postive test result given cancer.
they are very different probailities although sound the same. its like the diffference between “a 1 in a billion chance a human is the pope” and “a 1 in a billion chance the pope is human”